《Frontiers of Optoelectronics》期刊近日发表了北京理工大学路翠翠课题组撰写的有关典型拓扑光子晶体贝利曲率(Berry curvature)和陈数(Chern number)的通用数值计算方法的论文，该工作采用规范不变方法与拓扑光子晶体的有限元方法仿真相结合，实现了光子晶体Berry曲率和陈数的计算。

研究背景

拓扑光子学的研究表明，具有非平庸拓扑的光子晶体体系能够表现出许多优良性质，例如，在具有不同拓扑的光子晶体界面处，存在鲁棒的单向界面态，该界面态可以免疫缺陷与折角对界面态的散射，具有很低的传输损耗。因此，拓扑光子学在光子器件的设计方面具有广泛的应用价值。陈数是描述一类打破时间反演对称的光子晶体体系拓扑性质的重要参数，利用陈数，可以判断打破时间反演对称光子晶体的拓扑态，从而为构建鲁棒的界面态带来指导。因此，陈数的计算在光子晶体拓扑性质的理论预测和拓扑光子晶体器件设计的方面都具有重要价值。

北京理工大学物理学院路翠翠研究员课题组在论文中采用规范不变的link variable方法与光子晶体的FEM仿真相结合，实现了光子晶体Berry曲率和陈数的计算。该算法具有较强的通用性，适用于各种常见晶格结构和各种常见材料的光子晶体结构。利用陈数和Berry曲率的计算结果，本文讨论了结构形状、占空比与旋转角度对光子晶体陈数和Berry曲率的影响；此外，对于保护时间反演对称的拓扑，本文也演示了鲁棒的拓扑边界态与Berry曲率分布的关系。该工作为光子陈绝缘体(Chern insulator)的判断提供了一个简便、高效的方法，有助于实现基于拓扑态的器件设计。

内容简介

本文阐述了北京理工大学路翠翠课题组的陈数与Berry曲率的数值计算算法，并对主要计算结果进行分析与讨论。本文内容包括算法的介绍，常见光子晶体结构的Berry曲率、陈数计算结果，对陈数与Berry曲率影响因素的讨论和鲁棒的拓扑边界态的演示。

图文导读

图1. 正方布里渊区的离散化。

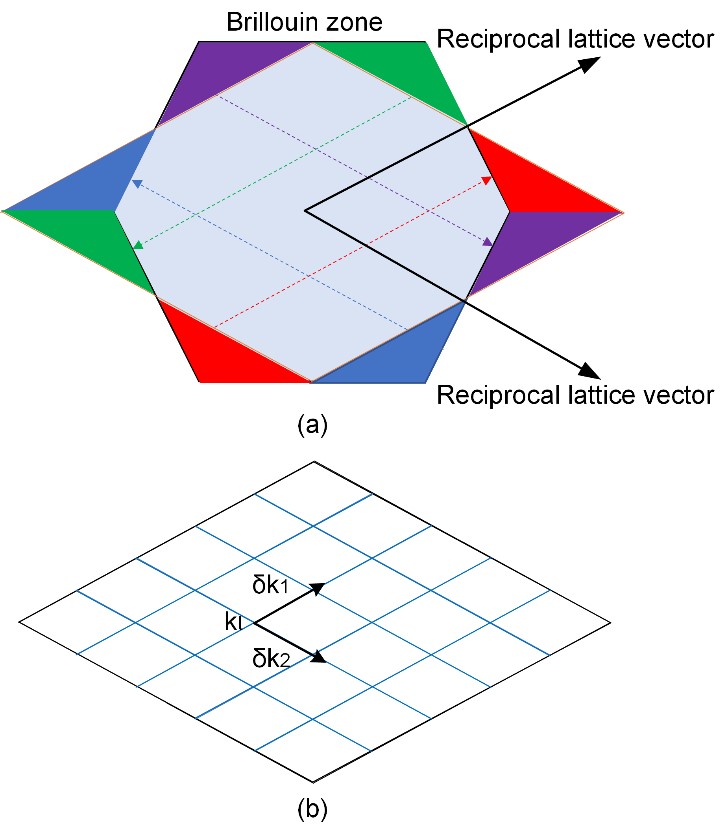
图2. 非正方布里渊区的等价变形和离散化。

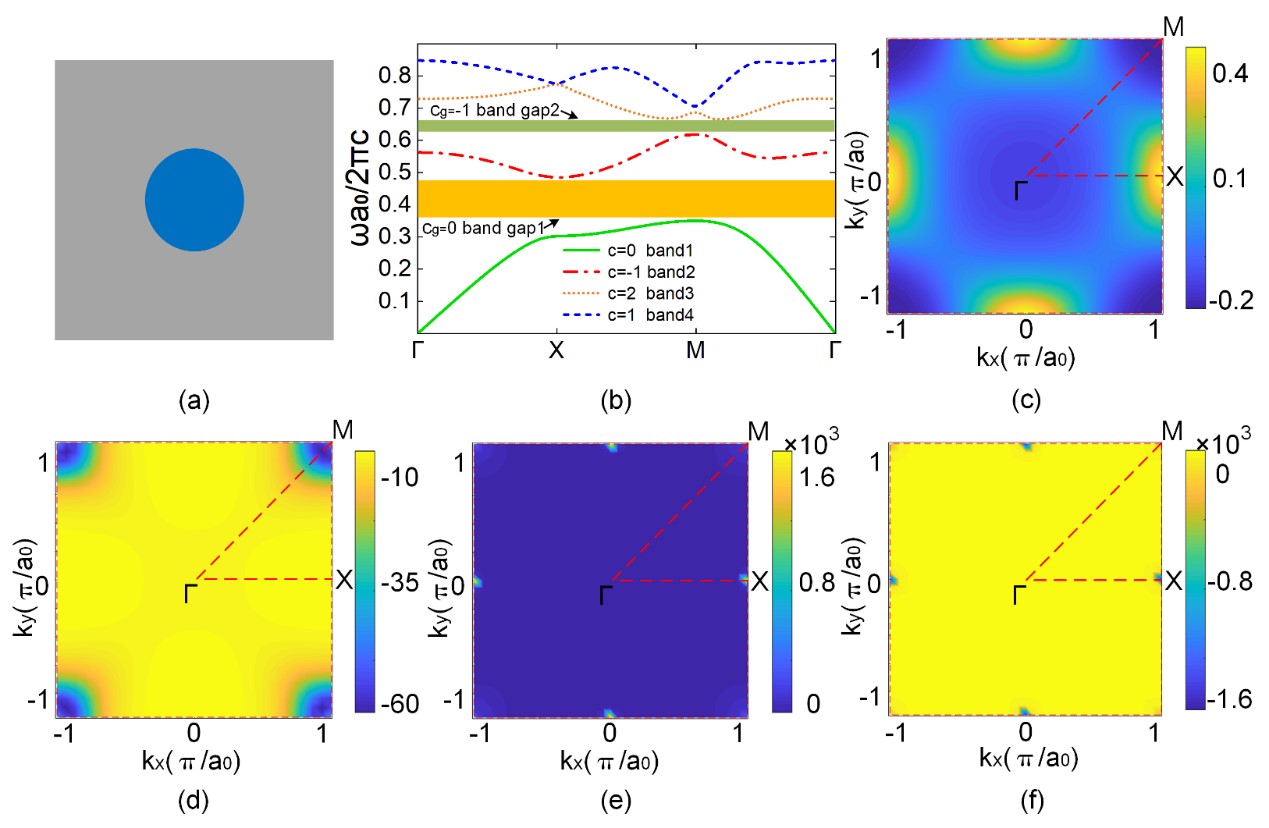
                         图3. 正方晶格旋磁材料圆柱结构TM模式的能带、陈数和Berry曲率分布。(c-f)分别为前四个TM模式能带的Berry曲率在第一布里渊区的分布。

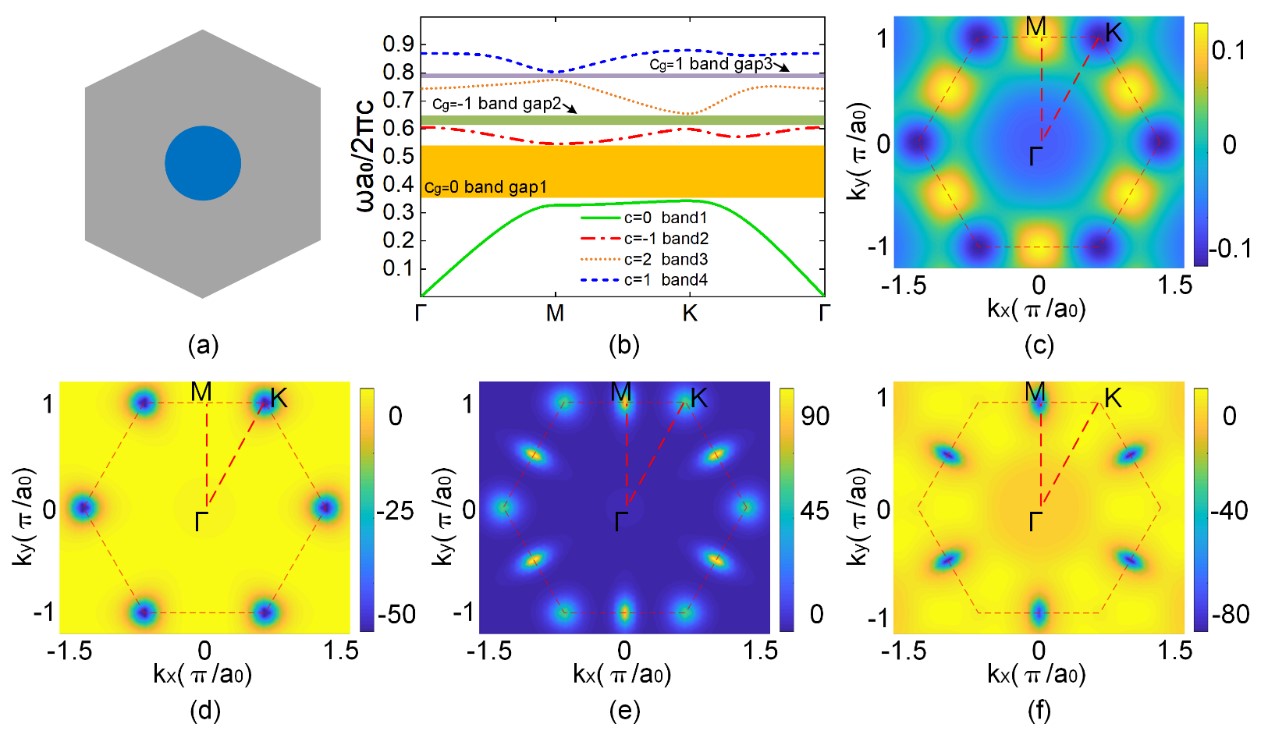
图4. 六角晶格旋磁材料圆柱结构TM模式的能带、陈数与Berry曲率分布。(c-f)分别为前四个TM模式能带的Berry曲率在第一布里渊区的分布。

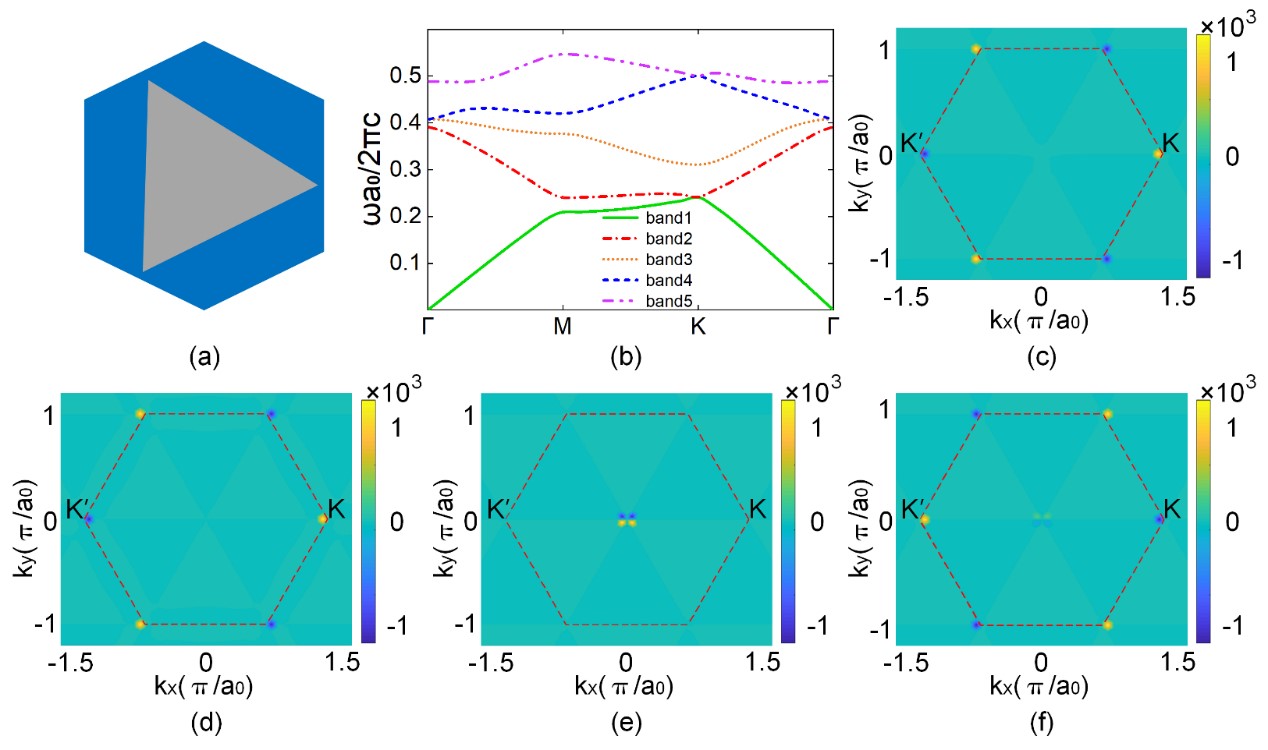
图5. 六角晶格介质板三角孔结构TM模式能带与Berry曲率。(c-f)分别为前四个TM模式能带的Berry曲率在第一布里渊区的分布。

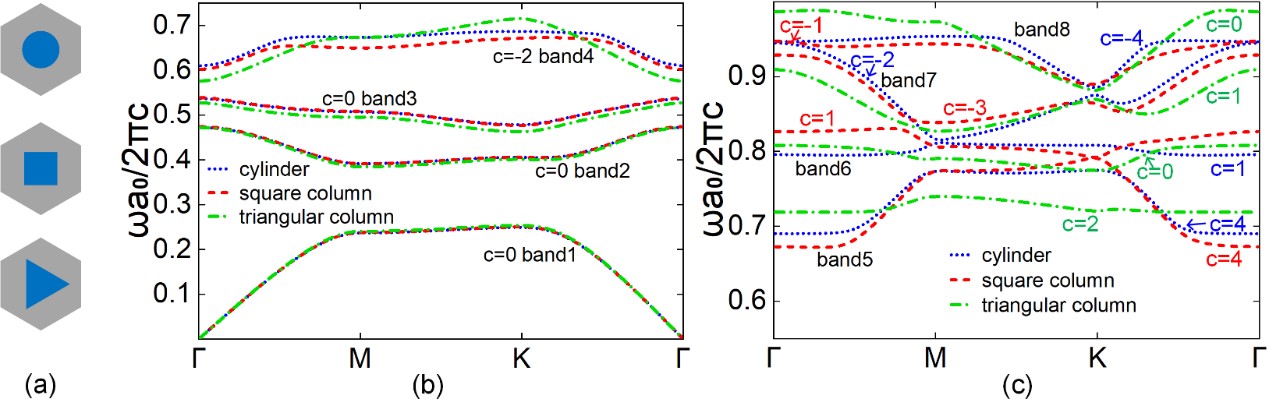
图6. 相同晶格与占空比，不同形状的旋磁材料柱结构的能带与陈数对比。(b-c)中不同曲线分别代表圆柱、四棱柱、三棱柱结构的能带。

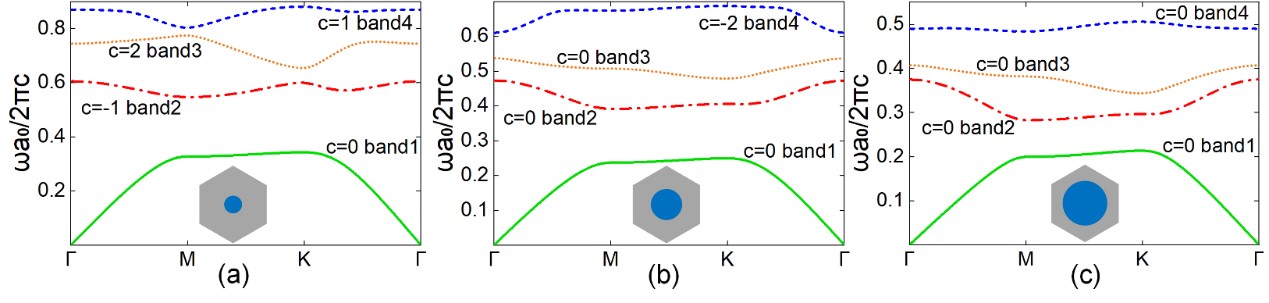
图7. 相同晶格与形状，不同占空比的旋磁结构能带与陈数对比。(a-c)分别为半径r=0.13a, r=0.23a, r=0.33a旋磁材料圆柱的TM能带与陈数。

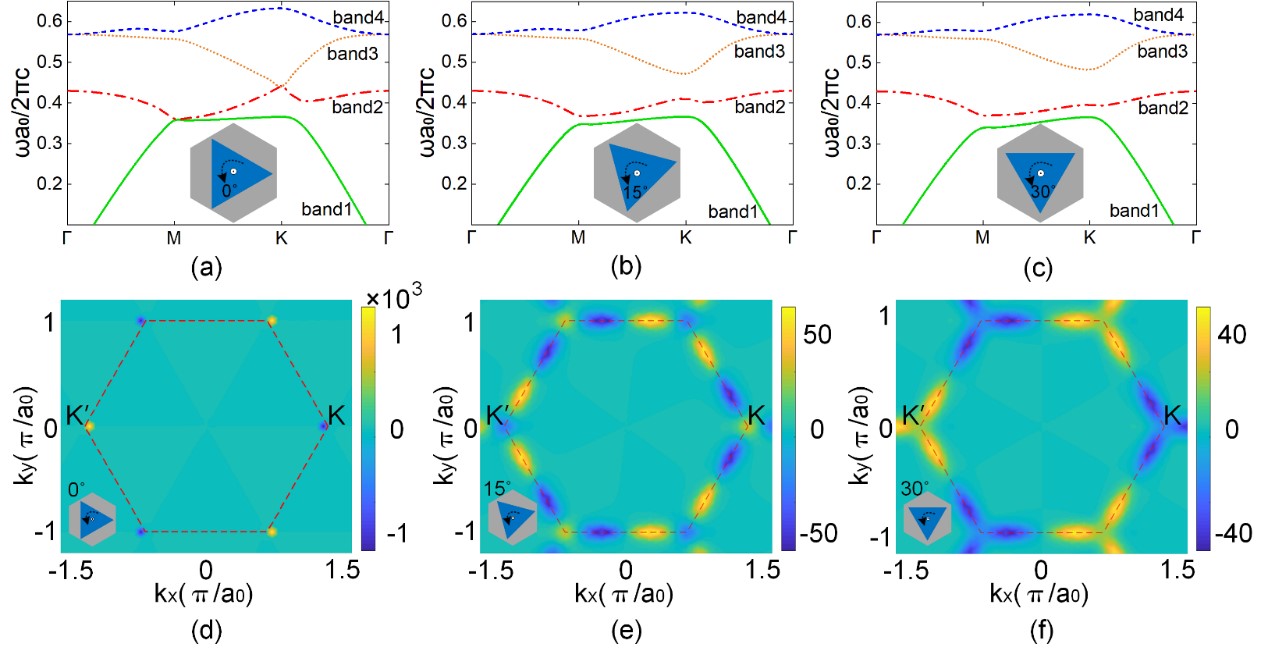
图8. 六角晶格纯介质三棱柱结构不同旋转角度对Berry曲率的影响。

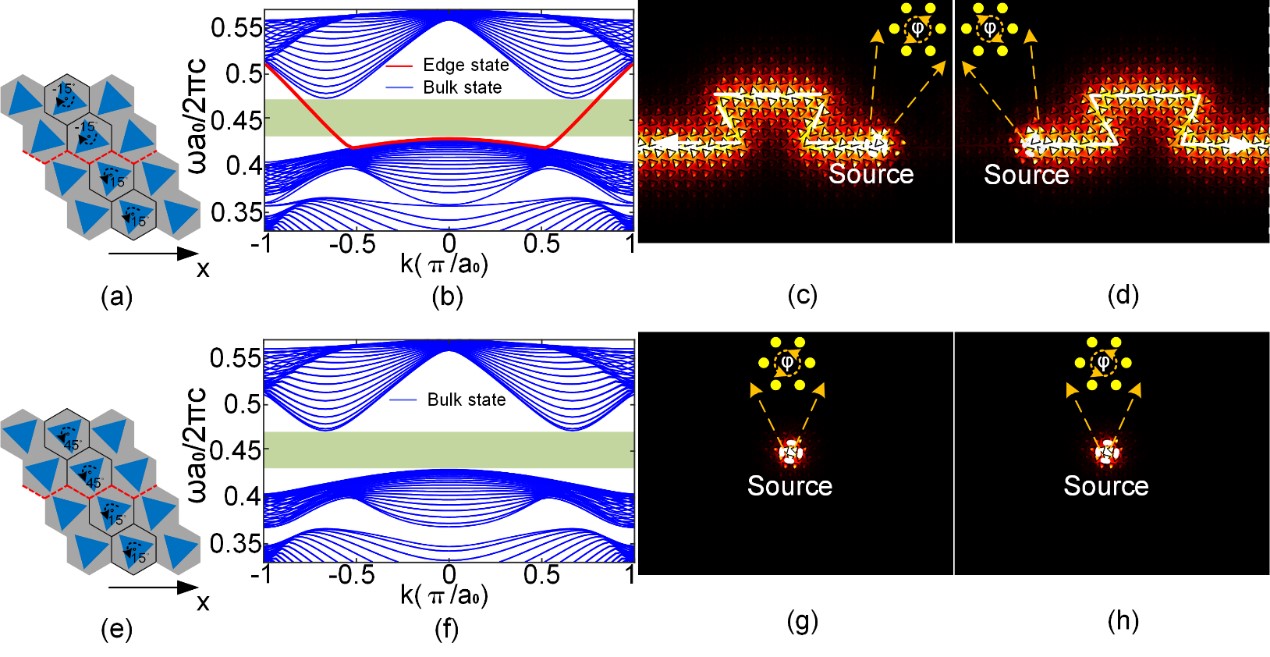
图9. 非陈绝缘体拓扑边界态的演示。(a-d)拓扑性质不同的光子晶体界面的性质，存在边界态。(e-h)拓扑性质相同、结构不同的光子晶体界面的性质，不存在边界态。

作者简介

通讯作者：路翠翠，2018年进入北京理工大学物理学院工作，任副研究员，博导，2015年博士毕业于北京大学物理学院，导师为胡小永教授，2020年2月至5月在香港科技大学C. T. Chan教授组访问。在微纳全光器件和拓扑光子学方向开展了多项研究，取得了一系列成果。在Physical Review Letters、Light: Science & Applications、Optica、Advances in Optics and Photonics、Laser&Photonics Reviews等国际权威期刊发表学术论文30余篇，主持国家自然科学基金项目2项，主持北京理工大学青年教师学术启动计划1项，参与国家自然科学基金重点项目2项，获得授权的国家发明专利3项，受邀担任华为中央研究院顾问、美国光学学会Optics Letters期刊编委（Topical Editor）。常年招聘博士后和研究生，欢迎发邮件联系cuicuilu@bit.edu.cn。

第一作者：王晨阳，北京理工大学物理学院2017级本科生，已保送为清华大学物理系2021级直博生。研究兴趣主要是拓扑光子学和纳米光学。曾获国家奖学金、2019年物理秋季学术会议优秀海报奖。自大二开始在路翠翠课题组从事本科生科研，已发表SCI论文2篇，申请国家发明专利一项。