共同第一作者：成骏伟、赵雨赫

通讯作者：董建绩

通讯单位：华中科技大学武汉光电国家研究中心

研究背景

随着人工智能技术的飞速发展，对高性能计算的需求日益迫切，光计算由于其固有的高速和低功耗的特点，以及其基于波分复用的并行处理能力，被视为部分取代电学计算从而实现计算加速的重要途径，受到了学术界和工业界的广泛关注。作为一种重要的基本计算操作，矩阵向量乘法被广泛应用于光学信号处理和光子神经网络中。微环是一种结构紧凑的谐振器件，其传输系数对波长敏感，因此可以通过控制微环的谐振状态来实现非相干矩阵向量乘法计算。非相干计算的特点意味着微环阵列只能进行幅度调制而没有相位信息，在此前的研究中，微环阵列几乎都只用于实数域计算，复数域计算则很少受到关注。此外，受限于热串扰，超大规模的微环阵列难以实现。因此，如何基于小规模微环阵列实现大规模复数矩阵向量乘法计算，是一个很有价值的研究课题。

文章简介

近期，华中科技大学张新亮教授研究团队提出了一种将基于微环阵列的矩阵计算从实数域扩展到复数域，从小规模扩展到大规模矩阵计算的解决方案，并且实验演示了Walsh-Hardmard变换、离散余弦变换、离散傅里叶变换和图像卷积处理。相关工作于2022年4月28日以A small microring array that performs large complex-valued matrix-vector multiplication为题发表在Frontiers of Optoelectronics期刊。

图文导读

1.工作原理与器件制作

图1展示了基于小规模微环阵列实现大规模复数矩阵向量乘法计算的工作原理。片上光子复数矩阵核由一个可调硅基微环阵列构成，该阵列包括16个经过精心设计的微环，按照4行4列进行排布。整个架构基于波分复用和片上可重构微环阵列，模拟一个4*4传输矩阵的完整网络，其参数配置可以通过热调谐每个微环来实现。首先，传输矩阵和输出向量通过差分方式从非负数域到全实数域的扩展，输入向量通过矩阵分解拆分为包含所有正元素的向量和包含所有负元素向量绝对值向量，最终实现将一个实数域的矩阵向量乘法拆分为两个非负数域的光学向量积运算和一次电学差分。在此基础上，进一步地将输入向量和传输矩阵拆分为实部和虚部，并将实部与虚部的运算分别进行，可最终得到四个光学矩阵向量积。因此，只需要在光域中分别计算这四个矩阵向量积，辅以电学差分，即可将微环阵列这一典型的非相干计算架构的计算域从非负数域拓展至复数域。此外，运用矩阵分块，结合电学设备的重组算法，可以进一步扩大矩阵向量乘法的规模，通过将大规模矩阵拆分为与计算硬件适配的矩阵块，可以在4*4规模的微环阵列上实现大规模的矩阵向量乘法。

研究团队在SOI平台上进行了微环阵列的制作，使用的SOI晶圆总厚度为725μm，其中顶层硅的厚度为220nm，掩埋氧化层的厚度为2μm。使用EBL将版图转移到光刻胶上，并通过ICP蚀刻顶部硅。光栅耦合器采用70nm浅刻蚀，硅波导采用220nm全刻蚀。在波导和金属电极之间，使用PECVD沉积了1μm的二氧化硅。金属电极和导线由EBE沉积得到。

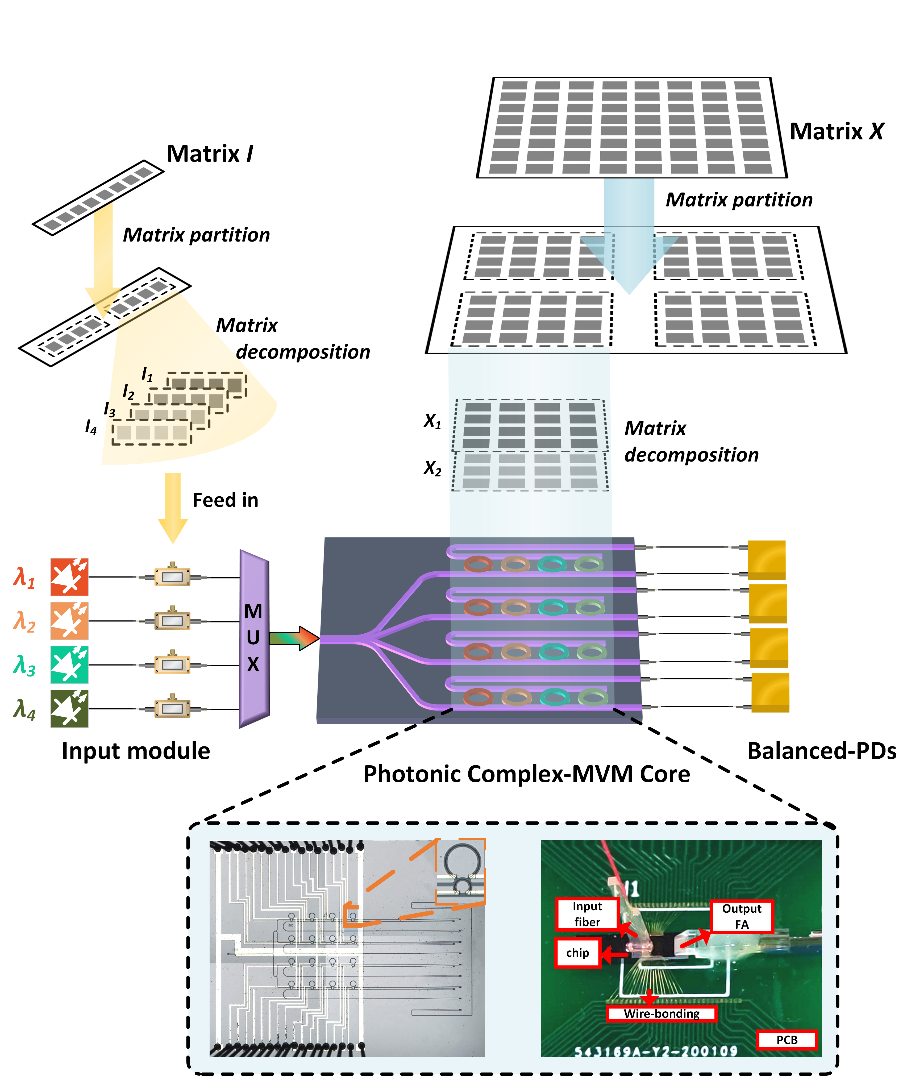
图1.光子复数矩阵向量乘法芯片的工作原理

2.在信号变换和图像处理中的应用

矩阵向量乘法是信号处理领域的一种基本计算操作。本文演示了三种典型的信号变换，分别是Walsh-Hardmard变换、离散余弦变换、离散傅里叶变换，三种信号变换的实验结果如图2所示。从实验结果可以看出，实验值与理论值基本吻合，表明我们的光子复数矩阵向量乘法芯片在实现信号变换时的计算误差很小。

图2.信号变换实验结果。WHT变换的(a)原始信号，(e)实验结果和理论值。偶对称DCT变换的(b)原始信号，(f)实验结果和理论值。前述序列一半的DCT变换的(c)原始信号，(g)实验结果和理论值。DFT变换的(d)原始信号，(h)实验结果和理论值

图像卷积在卷积神经网络和图像处理应用中至关重要，可以在光域中实现卷积加速。我们使用光子复数矩阵向量乘法芯片实验演示了图像卷积。我们选择武汉光电国家研究中心（WNLO）的标志作为示例，并分别使用7种不同的3*3卷积核对原图像进行处理。图3展示了实验结果，包括图像卷积结果和卷积核对应的传输矩阵。

图3.图像卷积的实验结果。(a)原始图像。不同卷积核处理得到的图像：(b)模糊，(c)动态模糊，(d)锐化，(e)左侧边缘提取，(f)右侧边缘提取，(g)上边缘提取，(h)下边缘提取

总结与展望

本文展示了一个小规模微环阵列，通过矩阵分解和矩阵分块算法，它可以执行大规模复数矩阵向量乘法计算，而且展示了其在(1)实数域、(2)复数域和(3)更高的处理维度中的典型应用。我们在SOI平台上制造了集成光子复数矩阵向量乘法芯片，与CMOS兼容。一个原本只能实现4×4矩阵计算的小规模微环阵列，可以扩展到传统非相干计算的复数域中的8*8、16*16甚至更高的运算维数。我们将该芯片应用于Walsh-Hardmard变换、离散余弦变换、离散傅里叶变换等信号变换，还实验演示了7种不同的图像卷积处理，并且在这些应用中展示出良好的性能。该芯片的处理能力可以通过并行计算以及与片上光源、微电子控制器实现光电混合集成来进一步增强。

论文下载网址：

https://link.springer.com/article/10.1007/s12200-022-00009-4