华中科技大学陈云天教授课题组：双各向异性光学结构中电磁有限元仿真

第一作者：熊仲非

通信作者：陈云天

通讯单位：华中科技大学光学与电子信息学院

研究背景

双各向异性超材料和双各向异性超表面的发展极大地促进了人们对复杂光学结构中光传输的理解，并推动了众多相关的应用，如谐振器、新奇的光学折反射以及光学拓扑绝缘体等。人们通常从超材料或超表面的结构单元中得到等效的本构参数，从而简化问题并易于分析电磁场性质。然而，目前计算双各向异性介质的方法仅限于解析方法，其计算过程复杂，且仅适用于简单结构。对于任意形状的双各向异性结构，缺乏一种通用的数值仿真方法。本工作填补了这一空白，提出了一个有限元数值方法来实现双各向异性结构中电磁特性的仿真。

内容简介

本文证明了含有双各向异性的矢量波动方程在标量内积下是自伴随的，并在实际应用中提出了一种平衡形式的弱形式方程，该方程在有限元模拟中优于标准的弱形式方程，能实现更准确的双各向异性情形下的仿真。在实际应用中，可在常见的商业有限元软件（如COMSOL）中将弱形式方程修改为本文提出的平衡形式的弱形式方程，即可仿真各种复杂的双各向异性光学结构的电磁性质。

图文简介

论文通过3个例子来验证平衡形式弱形式方程的有效性。如图1所示，在双各向异性均匀平板中，人们可以解析得到平面波入射时的TE/TM偏振光的透射率和反射率，且透反射率和双各向异性的参数十分相关。采用平衡形式弱形式方程的有限元仿真结果和解析得到的透反射率曲线完全一致，证明方程的有效性。

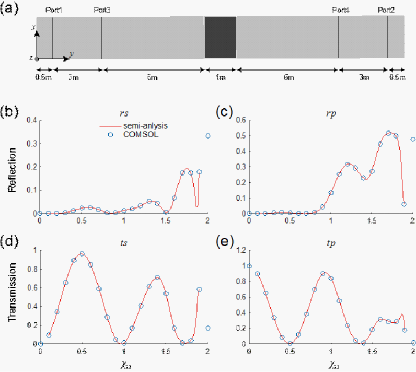
图1.双各向异性平板的折反射。（a）结构示意图，深灰色为双各向异性平板，浅灰色为空气。（b,c）s(p)偏振光的反射谱。（d,e）s(p)偏振光的透射谱。其中红色曲线为半解析结果，蓝色圈为COMSOL使用平衡弱形式的仿真结果

在双各向异性光子晶体中（图2），双各向异性打破空间反演对称性产生光学谷霍尔效应。论文利用平衡形式的弱形式方程计算的光子能带和参考文献给出的结果完全一致，进一步证明了本论文提出的有限元计算方法在双各向异性光学结构电磁特性仿真中的有效性。

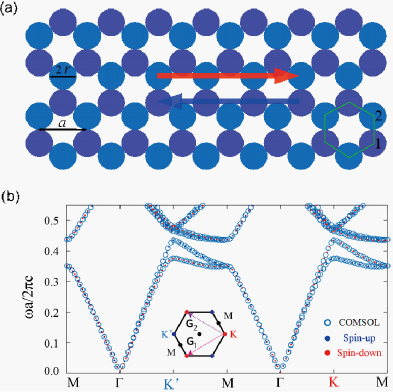
图2.（a）双各向异性光子晶体结构示意图。（b）参考文献（实心点为参考文献）和平衡弱形式的仿真结果（空心圈）的能带图

图3研究了双各向异性波导中的光学自旋轨道耦合效应。在双各向异性波导或环腔中，本征模式的偏振态一般为椭圆偏振光，偏振态与双各向异性的参数息息相关。因此双各向异性环腔可以实现特定偏振的光学隔离器。通过仿真双各向异性环形谐振腔的模态特性，产与理论预测一致的偏振依赖的光学隔离现象，即椭圆偏振光只能从左往右传播而不能从右往左传播，而螺旋度相反的偏振光则是只能从右往左传播而不能反向传播，理论分析的结果和图3的仿真结果完全一致。

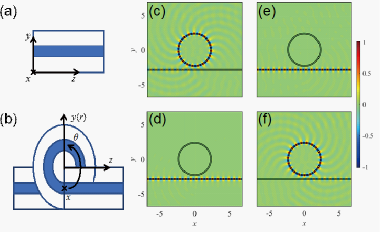
图3.双各向异性环腔作为特定偏振的光学隔离器（a,b）为双各向异性波导（a）和由波导卷曲形成的环腔（b）。（c-f）给出了偏振依赖的光隔离现象的仿真结果，图（c,d）中偏振方向为Ez+1.72iEy，图（e,f）中偏振方向为Ez+1.72iEy，图（c,e）中光从左向右传输，图（d,f）中光从右向左传输

总结

本工作建立的双各向异性结构的有限元仿真方法，为研究双各向异性引起的光学现象提供了有效的仿真手段，也为人们设计和研究更加复杂的双各向异性超材料和超表面提供了支持。

作者介绍

陈云天，华中科技大学光电学院副教授，博士生导师。 2005年获天津大学学士学位，2007年获浙江大学硕士学位，2010年获得丹麦科技大学博士学位。2011年-2013年在丹麦科技大学从事博士后研究，2013年入职华中科技大学光学与电子信息学院。在纳米光子学及电磁学计算，量子光学等相关领域发表包括Nature Comm, PRL, Light Science & Applications, NJP，PRB, OE, 和APL等SCI期刊论文50多篇。代表性工作包括解决了非厄米波导模式耦合问题中左矢空间和右矢空间不完备问题，构建了互易波导模式耦合理论；针对复杂光学环境中的光传输及偏振演化问题，提出了"非阿贝尔规范场光学"的理论框架以及光学系统的隐藏对称性；利用对称性原理揭示了有限尺寸散射体散射不变量特性，以及散射动量球上的强度、偏振奇点关联的绕数之和与庞加莱-霍福特定律的内在联系。研究方向包括复杂介质中光传输和散射现象，非线性光学系统光输运过程，光学数值计算方法，及光电器件的理论建模、仿真与设计优化，研究人工智能在光学及光电器件设计中的应用。

熊仲非，华中科技大学光学与电子信息学院在读博士生。2016在华中科技大学取得光电信息工程学士学位，目前参与发表论文十余篇。主要研究方向为拓扑光子学，自旋光子学和非线性系统中的光热力学。