第一作者（首选中文名）：Jack W. ZUBER

通讯作者（首选中文名）：Chao ZHANG

通讯单位：University ofWollongong

研究背景

近年来，具有拓扑序的材料得到了广泛的研究，特别是Dirac和Weyl材料，由于具有与拓扑特性相关的奇异的电学性质和量子输运，引起了人们的广泛关注。Weyl半金属（WSMs）是一类不具有时间反演对称性的拓扑材料，其对称破缺来源于动量空间中两个三维Dirac（Weyl）锥的分离。α-T₃模型可以描述为石墨烯和骰子（或T₃）晶格之间的一种二维晶格结构。对于二维和三维材料，无论是经典描述还是量子力学方法都表明，满足线性能量色散关系的带电载流子速度与动量不成正比，这导致不存在杂质散射时粒子与电磁场的耦合可以到无限级次，即具有很强的光学非线性响应。因此，即使在单电子模型中，Dirac系统也是一种强非线性材料。在二维Dirac系统，如石墨烯中，强的非线性效应已经得到验证，如光学混频、高次谐波产生（HHG）、表面等离激元与光的非线性耦合以及光学双稳态等；在三维Dirac材料和WSMs中，已经报道了太赫兹波段的光学混频和超快电荷动力学。

内容简介

近年来，具有拓扑序的材料得到了广泛的研究，特别是Dirac和Weyl材料，由于具有与拓扑特性相关的奇异的电学性质和量子输运，引起了人们的广泛关注。Weyl半金属（WSMs）是一类不具有时间反演对称性的拓扑材料，其对称破缺来源于动量空间中两个三维Dirac（Weyl）锥的分离。α-T₃模型可以描述为石墨烯和骰子（或T₃）晶格之间的一种二维晶格结构。对于二维和三维材料，无论是经典描述还是量子力学方法都表明，满足线性能量色散关系的带电载流子速度与动量不成正比，这导致不存在杂质散射时粒子与电磁场的耦合可以到无限级次，即具有很强的光学非线性响应。因此，即使在单电子模型中，Dirac系统也是一种强非线性材料。在二维Dirac系统，如石墨烯中，强的非线性效应已经得到验证，如光学混频、高次谐波产生（HHG）、表面等离激元与光的非线性耦合以及光学双稳态等；在三维Dirac材料和WSMs中，已经报道了太赫兹波段的光学混频和超快电荷动力学。

图文简介

进展1：考查两个系统的电子结构，引入描述其非线性性质的模型

采用最小耦合模型，可以给出二节点半金属的哈密顿量，该哈密顿量具有电荷和宇称不变性，对角化后得到能量色散曲线，如图1所示，其中图1(a)-(c)显示了v_Fb与带隙Δ的相对大小变化时其拓扑相的变化：从Weyl半金属（WSM）相变为三维有质量Dirac半金属（MDSM）相/无质量Dirac半金属（DSM）相，再变为带隙半金属（GSM）相。另一方面，由最小耦合模型下α-T₃晶格的哈密顿量可以得到三个波函数及其对应的能量本征值，其能量色散曲线如图2所示。

在量子态和能量色散的基础上，我们采用半经典输运方程和量子密度矩阵方法计算电流响应。从而得到非线性响应与如Weyl点分离量、带隙等重要参数的关系。半经典方法中，可以采用速度算子的泰勒展开来计算非线性电导率；而量子力学方法中，与各阶电场相关的项中必须同时考虑哈密顿矩阵元的阶次和约化密度矩阵的阶次。这两种方法可以方便地得到非线性效应对于上述固有参数的依赖关系。

图1二节点半金属的能量色散（a）WSM相，其中箭头表示电场平行于Weyl点分离量b时两种带内电流的贡献（b）MDSM相，DSM相是其中的一个特殊情况（c）GSM相。

图2 α-T₃晶格的能量色散，图中右侧给出了两种带间跃迁和一种带内跃迁

进展2. 太赫兹波段两种材料非线性电导率的理论计算结果

由于最小耦合模型下WSM和α-T₃系统的哈密顿量都是宇称对称的，因此二阶非线性电导率为0，三阶非线性是最低阶的非线性项。若忽略三阶以上的非线性项（对于高频率、低电场的情况是合理的），则可以用线性电流与三阶电流大小相等时的电场强度来定量计算非线性项的大小，称为临界电场。

2.1WSM的非线性电导率

我们阐明了WSM哈密顿量的非线性响应对于其拓扑相（WSM、MDSM/DSM或GSM）的依赖性，并进一步探讨了b≠0引起的各向异性。

我们首先计算了电场方向平行于b时，太赫兹波段的一阶和三阶电导率随带隙Δ和温度T的变化，如图3所示。图3（a）中，由于Δ不等于零破坏了沿b方向的色散关系，在Δ从零变为有限值时三阶非线性电导率有一个不连续的跳变。考虑到电导率中起主导作用的是锥内过程，由于费米速度的重整化，锥内过程随Δ的增加迅速减小，因此随着Δ的增加，拓扑相依次变为MDSM相（拐点处）和GSM相，一阶和三阶电导率也随之不断减小。与带隙的影响不同，锥间跃迁电流在温度对三阶电流的影响中起着非常重要的作用，如图3（b）所示。在温度较低时，锥间载流子与单光子的耦合更容易发生，因此在WSM相中电导率存在一个初始的下降过程。随着温度的升高，MDSM相和GSM相的一阶和三阶电导率随温度的增加而指数上升，三阶电导率开始上升的开关温度约为275K。

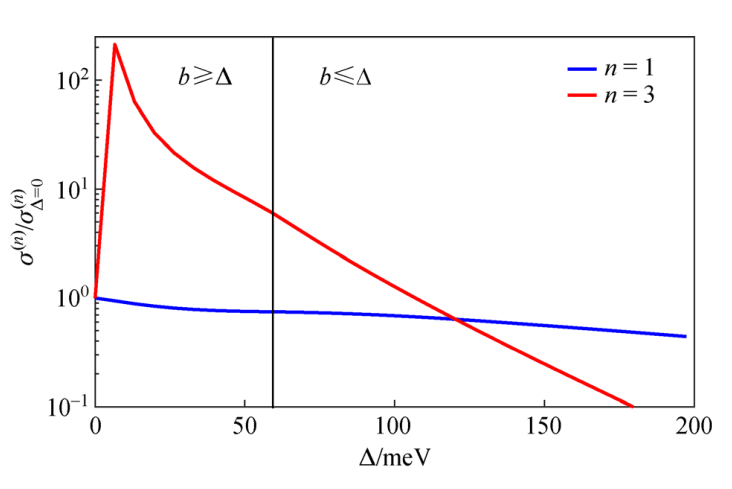
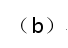
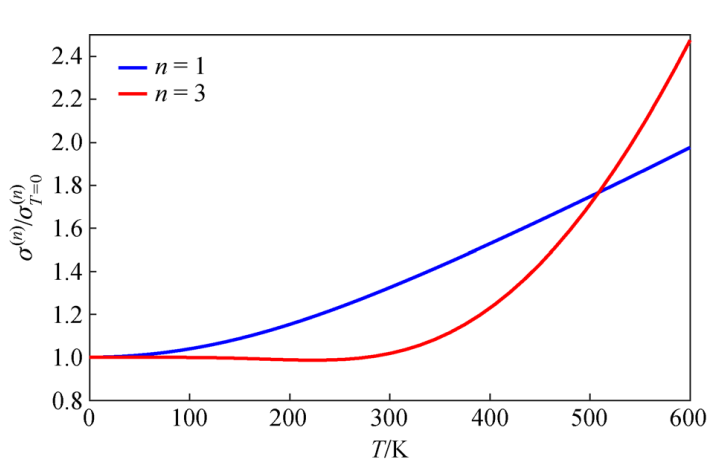
图3电场方向平行于b时，WSM在太赫兹波段的一阶和三阶电导率随带隙（a）和温度（b）的变化

我们进一步研究了电导率各向异性随带隙Δ 的变化，结果表明：一阶各向异性在WSM/MDSM相的交界面之前取得最小值，在GSM相中一阶垂直电导率更快地接近零，因此各向异性增加。三阶各向异性初始的尖峰是由于平行电导率的跳变引起的。当p=0 处的能量本征值等于E_F时，出现拐点；随后当垂直电导率达到最大值时，在WSM/MDSM相的边界处出现最小值。另外我们还计算了非线性各向异性随温度的变化，结果表明：在GSM相中，三阶非线性曲线在开关温度之后均不断增加。这一结果是具有实际意义的，因为它表明在较高的温度下会有较低的临界电场。

2.2α-T₃模型的非线性电导率

频域中α-T₃模型光学电导率的一阶特性如图4所示。如预期的那样，平带对α =0的电导率不起作用，E–价带对α = 1的电导率不起作用。对于α的中间值, 都存在E₀→E₊和E_–→E₊带间过程。对于每个α值，参数T、µ 以及Δ 扮演的角色是相同的：T的增加打破了霍尔量子化，平滑了阶跃函数，而µ 仅仅改变霍尔效应频率。带隙参数Δ则以更具拓扑意义的方式破坏量子化。首先，峰值变大，并产生sgn (µ – Δ)Δ的频移. 此外，与霍尔平台效应不同，导电率朝着Δ=0时的值逐渐降低。

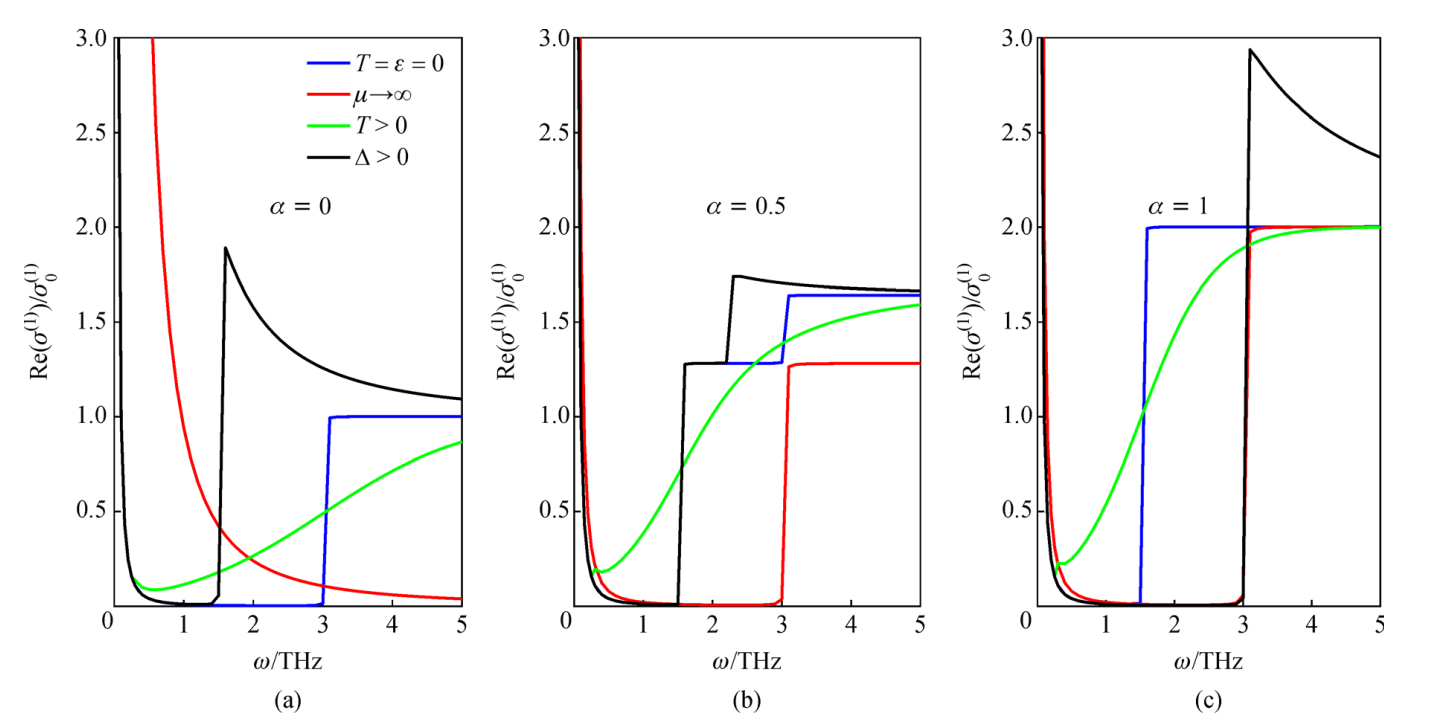
图4太赫兹波段α=0（a），α=0.5（b）和α=1（c）时α-T₃晶格的一阶电导率

三阶电导率包括来自3个带内过程和22个带间过程的贡献，我们考虑了带间响应中的五个独特谐波过程，给出了THz波段严格的响应，结果如图5所示。其中最显著的特点是：Berry相位取中间值时允许平带到导带和价带到导带三阶过程共存，这突出了HHG的内在的几何性质。通过调节Berry相位在0到π之间变化, 主峰位置会有一个数量级的波动，这个特性可用于构造可调谐的太赫兹接收器。

图5太赫兹波段不同Berry相位下α-T₃晶格的三阶电导率

非线性响应的另一个可能应用是利用主峰来确定Berry相位和表征晶体结构。为此我们还研究了α-T₃晶格中不同Berry相位下临界电场随频率的变化，以及不同频率下临界电场随Berry相位的变化。

【总结】

利用半经典模型计算了两节点半金属在WSM、MDSM和GSM相中的非线性带内电导率。结果表明，其非线性响应的主要特征取决于拓扑相，而拓扑相则取决于v_Fb和Δ的相对大小。利用量子力学模型计算了α-T₃晶格的非线性光学响应。一阶电导率在由拓扑相直接决定的频率处出现霍尔量子化，HHG也由拓扑相决定。Berry相位取中间值时的非线性特性使得可调谐非线性材料或者基于非线性响应的拓扑材料特性表征成为可能。

【作者介绍】

张潮教授现为澳大利亚伍伦贡大学终身教授、太赫兹光电与热电物理研究中心主任。他1987年获美国纽约市立大学物理学博士学位。1987年至1989年，在马克斯普朗克固体研究所凝聚态物理学家、诺贝尔奖获得者Von Klitzing教授课题组从事博士后研究，研究方向是半导体纳米结构中量子磁传输。1989年至1992年，在加拿大温哥华的Meson研究机构担任研究员，致力于固体量子相干性和耗散性的研究。1993年成为澳大利亚伍伦岗大学物理学院终身教授。研究方向为纳米结构的量子传输、太赫兹光子学、半导体的非线性动力学、石墨烯和拓扑绝缘体。他在光电子学、材料科学、凝聚态物理尤其在THz光电子学等领域做出了多项重要的工作，是国际物理学界公认的领导者之一。近年来他在研究石墨烯光电子学以及石墨稀中光电响应的关键问题方面取得了重要进展，是该方向的国际领军人物，在国际学术界具有广泛的影响力。在Phys. Rev. Lett., Phys. Rev., Appl. Phys. Lett.等国际学术刊物上发表论文220余篇。

课题组网站：

https://scholars.uow.edu.au/display/chao_zhang

第一作者介绍

Jack W. ZUBER，2017年获澳大利亚伍伦岗大学物理学学士， 2021年获澳大利亚伍伦岗大学物理学博士。主要研究方向为拓扑序的材料中的量子输运理论分析与数值计算。