本文介绍的是哈尔滨工程大学物理与光电工程学院王雷副教授课题组惯性梯度方法用于荧光分子层析成像，发表在《Journal of Innovative Optical Health Sciences》期刊2021年第2期。

Inertial gradient method for fluorescence molecular tomography

Lei Wang, Hui Huang

研究背景

荧光分子层析成像（fluorescence molecular tomography, FMT）是一种主要用于小动物临床前研究与人乳腺肿瘤早期诊断的新型光学成像技术。由于生物组织对可见光或近红外光具有强散射作用，FMT图像重建是高度病态的反问题，常常需要通过正则化方法降低重建问题的病态性。在近年来的FMT重建研究中，采用非平滑正则项的重建方法相比传统的平滑正则化方法能生成更好的图像重建质量和更高的图像重建精度。但是用于非平滑正则化重建反问题的优化算法的计算量很大，对重建算法的速度提出了很高的要求。

内容简介

本文以L1范数作为FMT重建的正则项，建立一种新型的重建算法（RIGA-R）。此算法包含了以下三种技术：Moreau-Yosida正则、惯性动力学加速与基于梯度的自适应重启。并与以下三种先进算法做了比较：Chambolle-Pock加速式一阶原始对偶算法（ACPM）、近端式优化梯度算法（POGM）与自适应重启式FISTA算法（FISTA-R）。通过大量数值仿真实验结果表明，与其它三种先进算法相比较，此算法能获得几乎完全一样的图像重建质量和精度，但是重建速度具有非常明显的提升。

图文导读

1.2D仿真实验

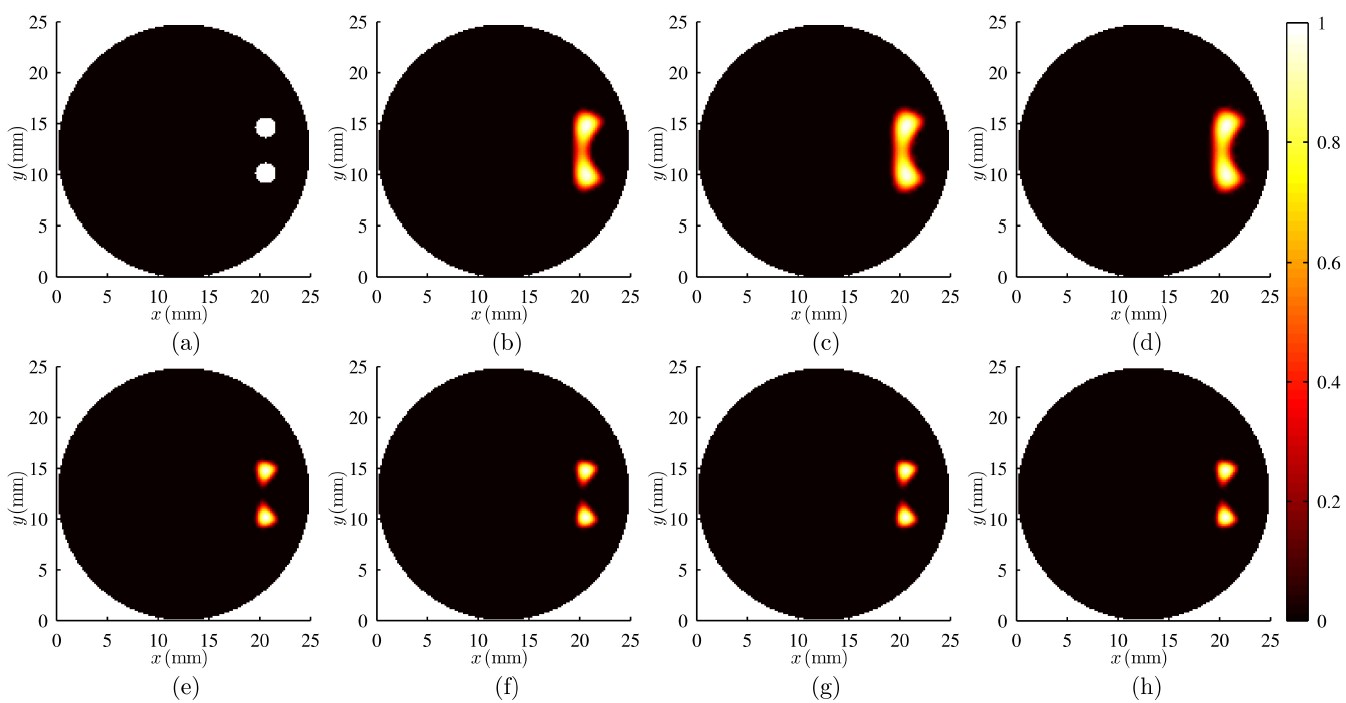
图1：2D仿真实验重建图像（荧光目标较浅，间距2.5mm，1%噪声）。（a）荧光目标。（e）RIGA-R。（b）（f）ACPM。（c）（g）POGM。（d）（h）FISTA-R。（e）-（h）采用相同的算法终止判据。（b）-（d）采用与RIGA-R相同的迭代次数。

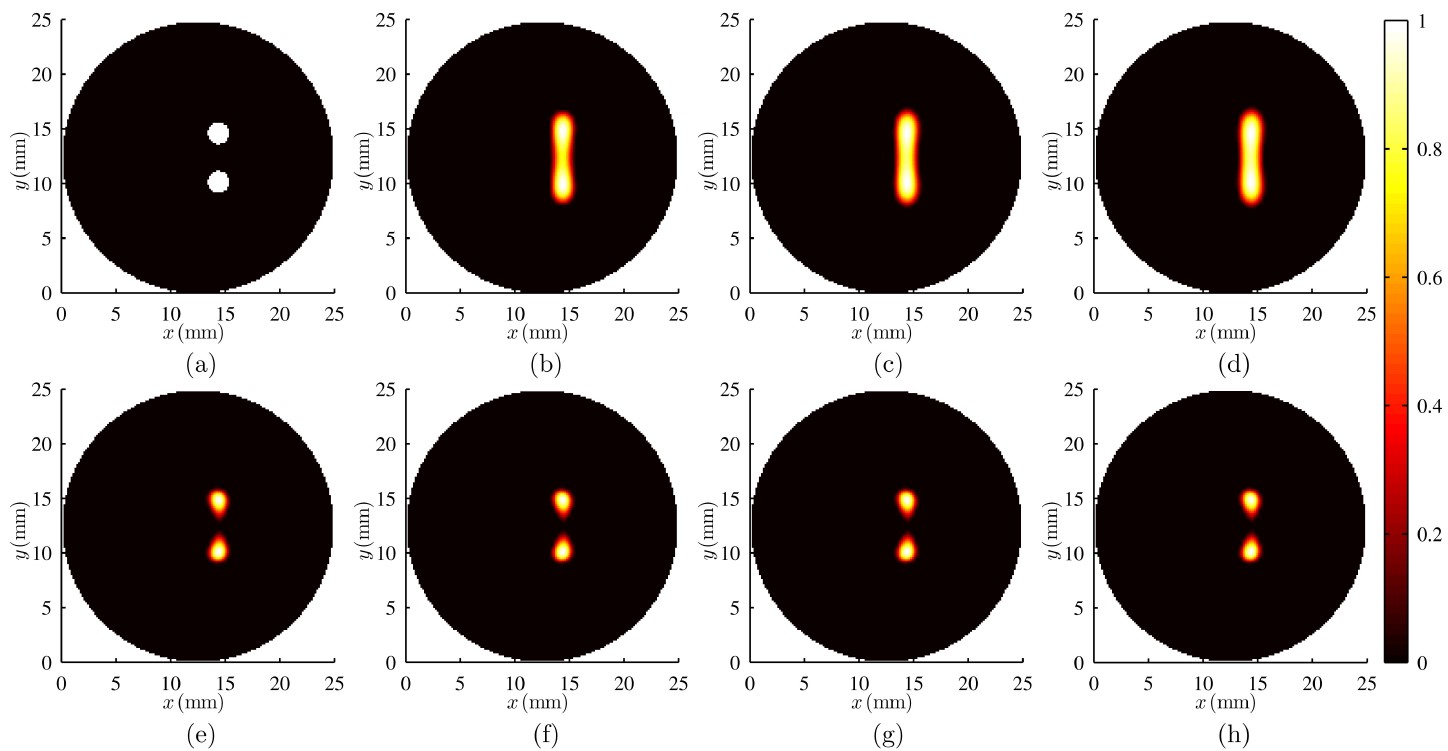
图2：2D仿真实验重建图像（荧光目标较深，间距2.5mm，1%噪声）。（a）荧光目标。（e）RIGA-R。（b）（f）ACPM。（c）（g）POGM。（d）（h）FISTA-R。（e）-（h）采用相同的算法终止判据。（b）-（d）采用与RIGA-R相同的迭代次数。

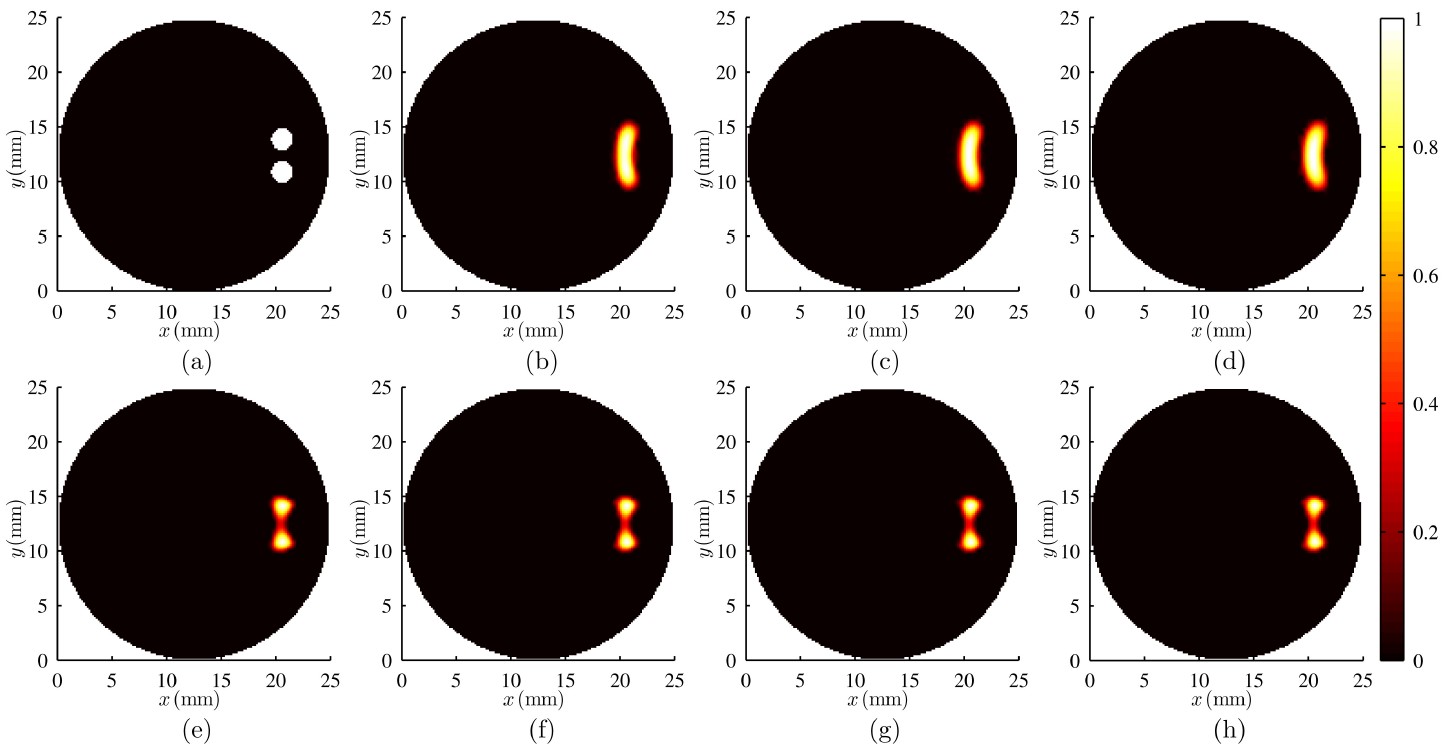
图3：2D仿真实验重建图像（荧光目标较浅，间距1mm，1%噪声）。（a）荧光目标。（e）RIGA-R。（b）（f）ACPM。（c）（g）POGM。（d）（h）FISTA-R。（e）-（h）采用相同的算法终止判据。（b）-（d）采用与RIGA-R相同的迭代次数。

图4：2D仿真实验重建图像（荧光目标较浅，间距2.5mm，5%噪声）。（a）RIGA-R。（b）（c）ACPM。（d）（e）POGM。（f）（g）FISTA-R。（a）（c）（e）（g）采用相同的算法终止判据。（b）（d）（f）采用与RIGA-R相同的迭代次数。

图5：2D仿真实验重建图像（荧光目标较浅，间距2.5mm，15%噪声）。（a）RIGA-R。（b）（c）ACPM。（d）（e）POGM。（f）（g）FISTA-R。（a）（c）（e）（g）采用相同的算法终止判据。（b）（d）（f）采用与RIGA-R相同的迭代次数。

图6：2D仿真实验重建图像（荧光目标较浅，间距2.5mm，25%噪声）。（a）RIGA-R。（b）（c）ACPM。（d）（e）POGM。（f）（g）FISTA-R。（a）（c）（e）（g）采用相同的算法终止判据。（b）（d）（f）采用与RIGA-R相同的迭代次数。

图1-图6中的2D仿真实验重建图像表明，如果采用相同的算法终止判据，本文提出的RIGA-R算法相比于其它三种算法能获得几乎完全一样的重建图像，但是只需要明显更少的迭代次数。

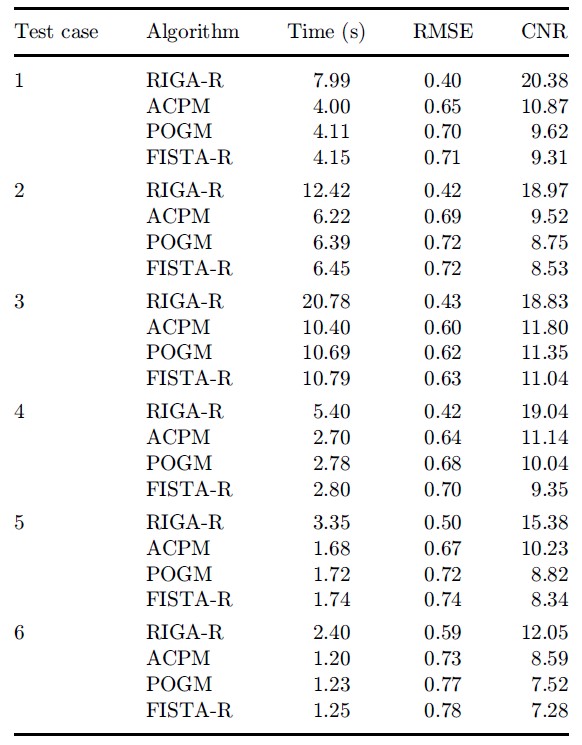
表2：2D仿真实验重建定量结果（四种算法采用相同的迭代次数）。

表2说明，2D仿真实验中，如果采用相同的迭代次数，本文提出的RIGA-R算法获得的图像重建精度（RMSE和CNR）远高于其它三种算法。

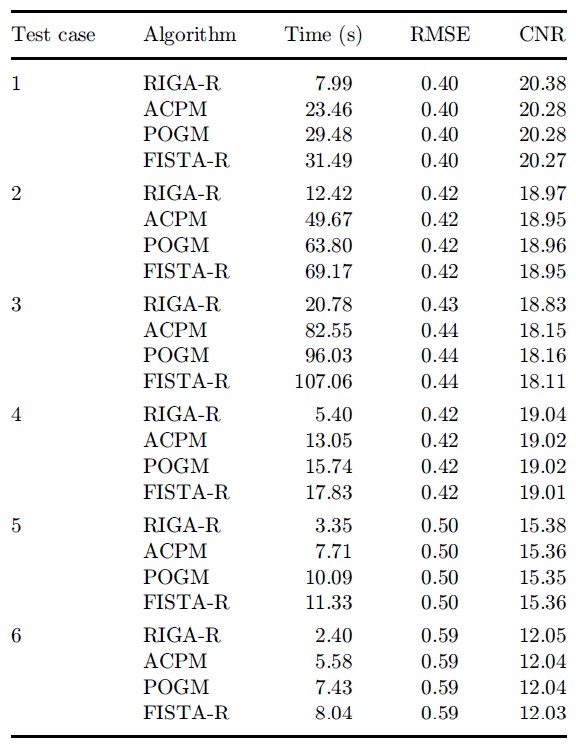
表4：2D仿真实验重建定量结果（四种算法采用相同的终止判据）。

表4说明，2D仿真实验中，如果采用相同的算法终止判据，本文提出的RIGA-R算法获得的图像重建精度（RMSE和CNR）与其它三种算法几乎完全相同，但是重建速度远快于其它三种算法。

2.3D仿真实验

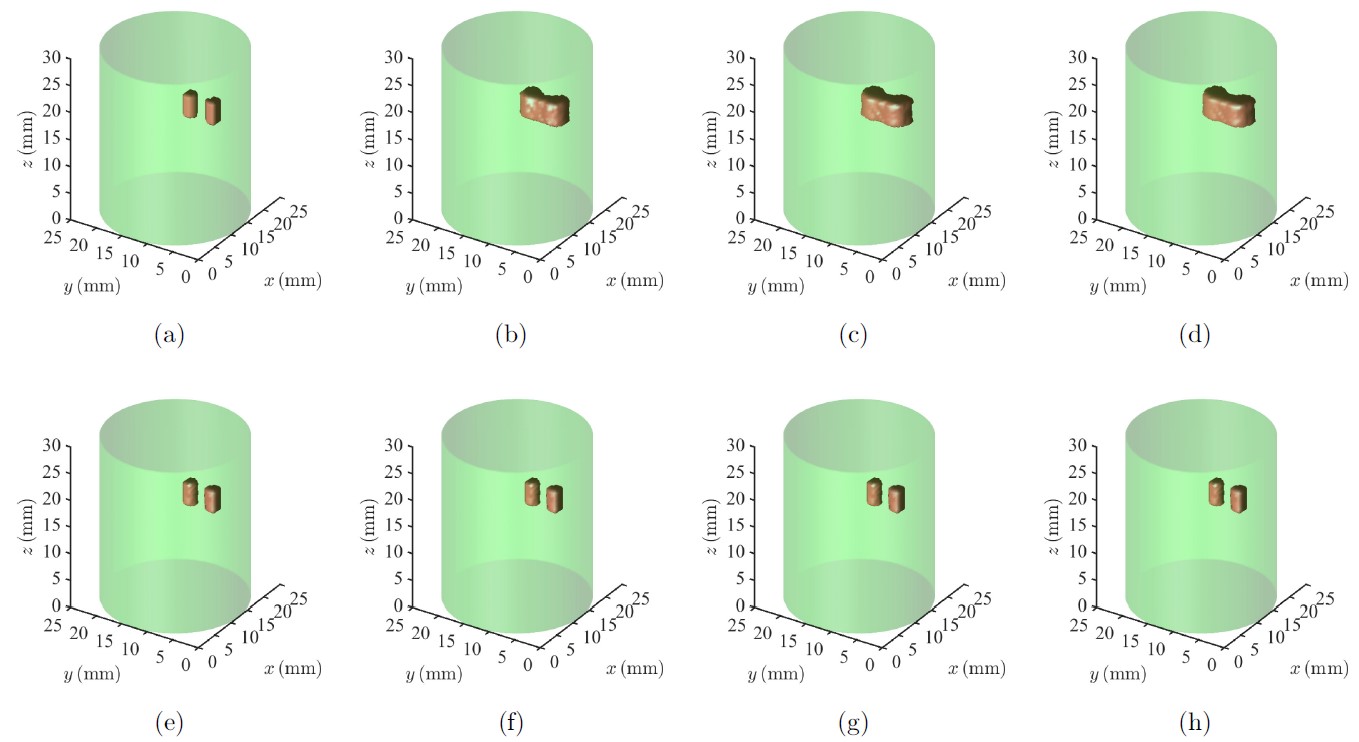
图7：3D仿真实验重建图像（荧光目标较浅，间距2.5mm，1%噪声）。（a）荧光目标。（e）RIGA-R。（b）（f）ACPM。（c）（g）POGM。（d）（h）FISTA-R。（e）-（h）采用相同的算法终止判据。（b）-（d）采用与RIGA-R相同的迭代次数。

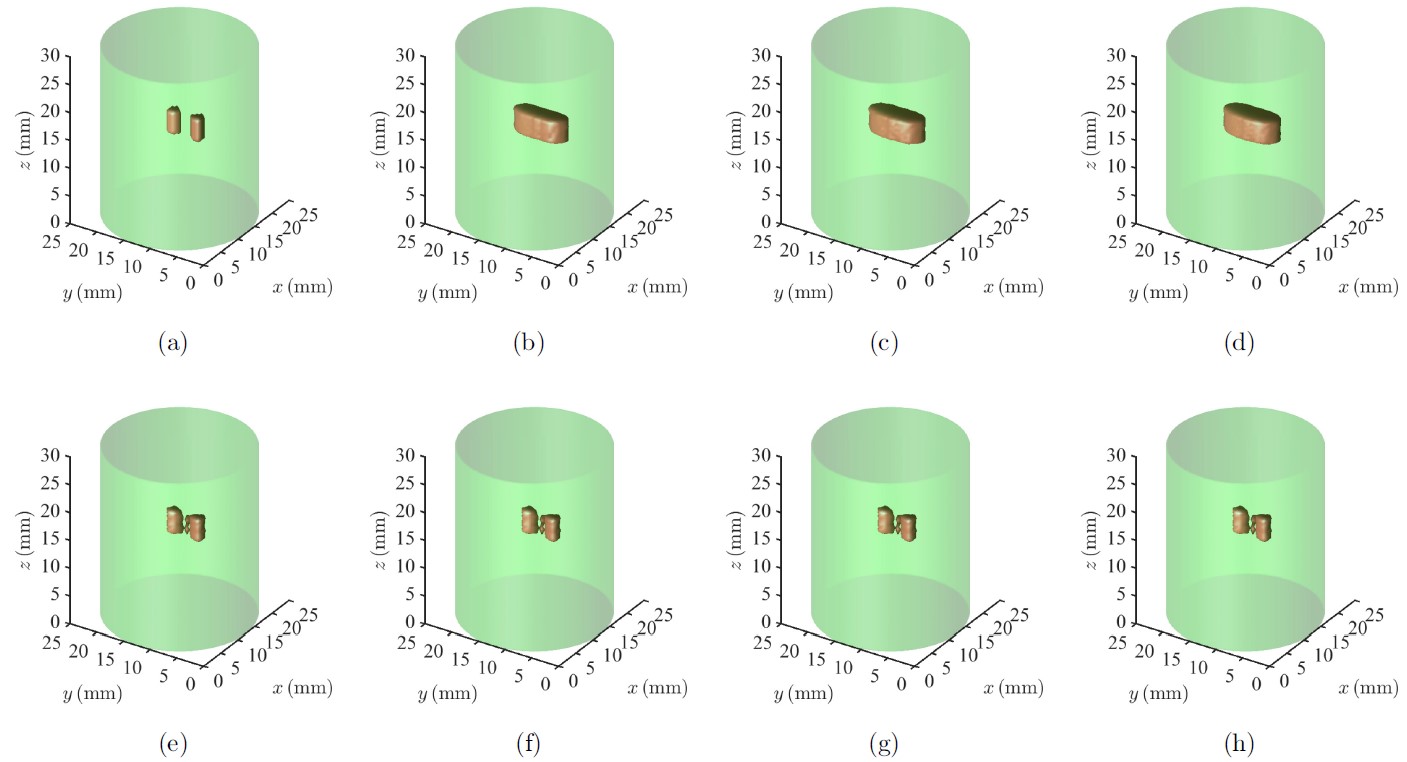
图8：3D仿真实验重建图像（荧光目标较深，间距2.5mm，1%噪声）。（a）荧光目标。（e）RIGA-R。（b）（f）ACPM。（c）（g）POGM。（d）（h）FISTA-R。（e）-（h）采用相同的算法终止判据。（b）-（d）采用与RIGA-R相同的迭代次数。

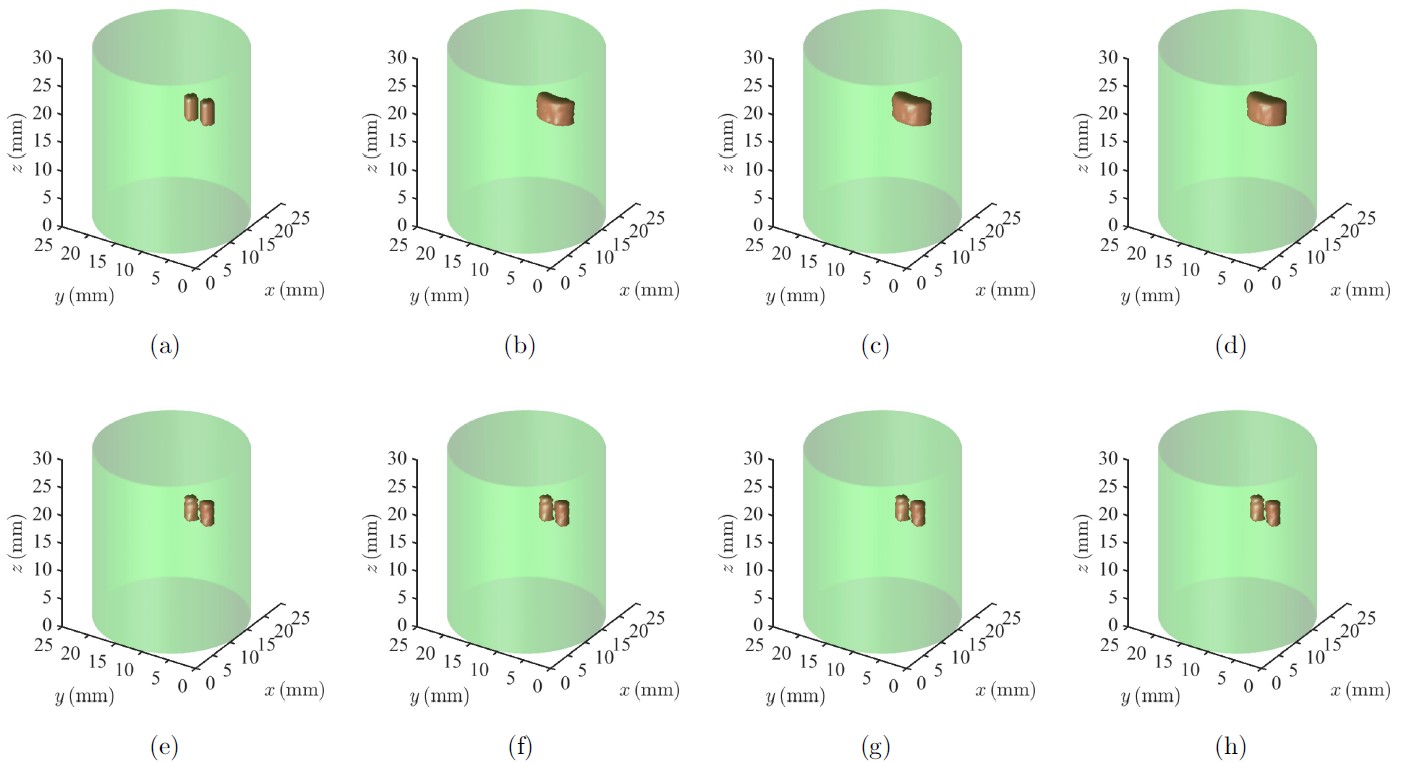
图9：3D仿真实验重建图像（荧光目标较浅，间距1mm，1%噪声）。（a）荧光目标。（e）RIGA-R。（b）（f）ACPM。（c）（g）POGM。（d）（h）FISTA-R。（e）-（h）采用相同的算法终止判据。（b）-（d）采用与RIGA-R相同的迭代次数。

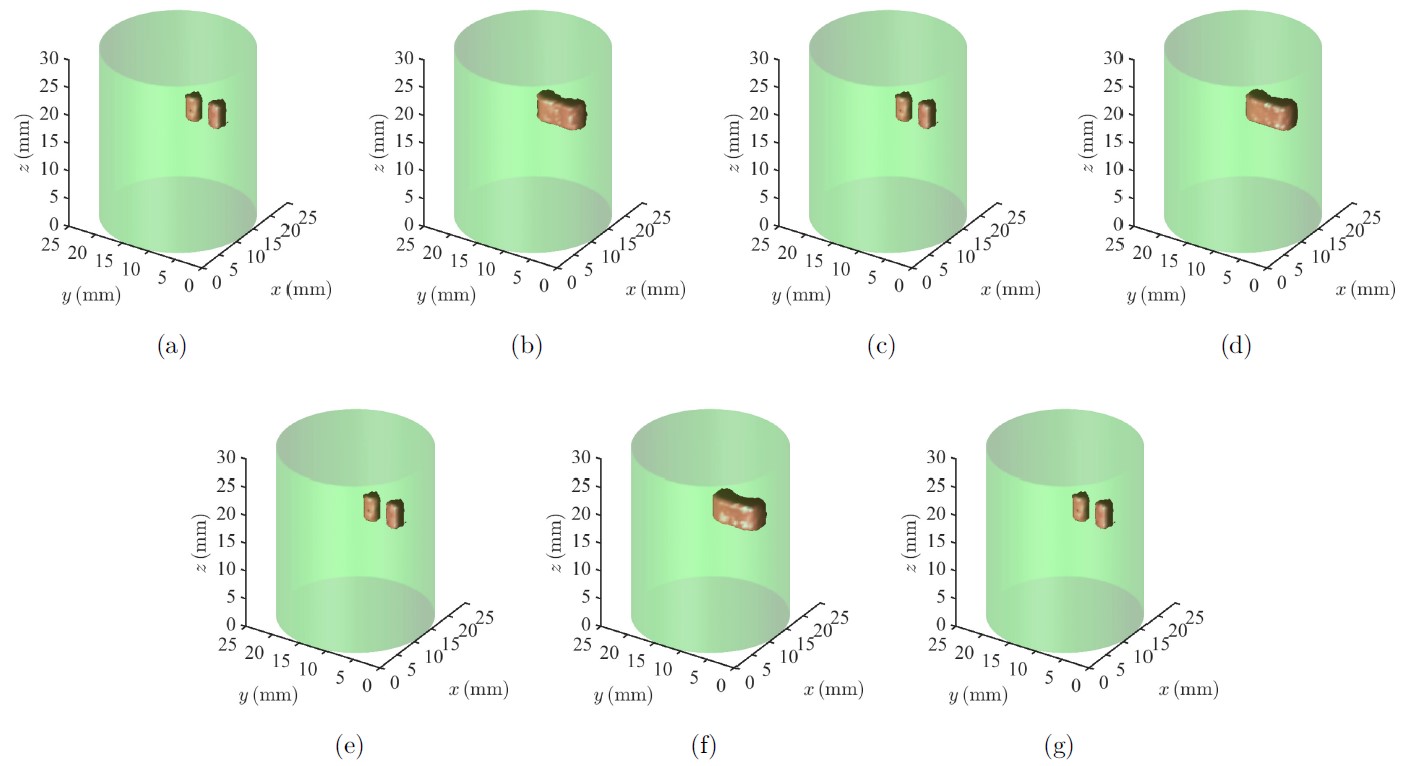
图10：3D仿真实验重建图像（荧光目标较浅，间距2.5mm，5%噪声）。（a）RIGA-R。（b）（c）ACPM。（d）（e）POGM。（f）（g）FISTA-R。（a）（c）（e）（g）采用相同的算法终止判据。（b）（d）（f）采用与RIGA-R相同的迭代次数。

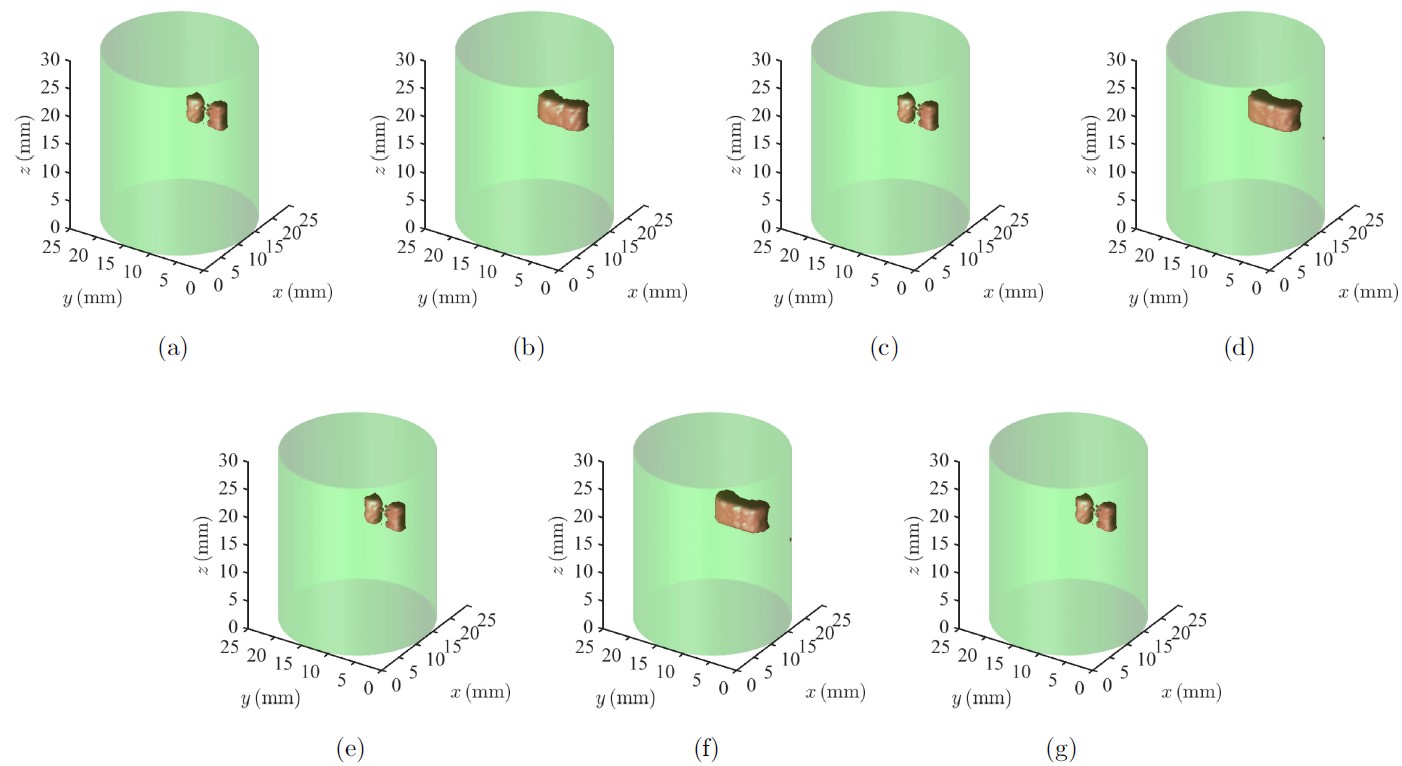
图11：3D仿真实验重建图像（荧光目标较浅，间距2.5mm，15%噪声）。（a）RIGA-R。（b）（c）ACPM。（d）（e）POGM。（f）（g）FISTA-R。（a）（c）（e）（g）采用相同的算法终止判据。（b）（d）（f）采用与RIGA-R相同的迭代次数。

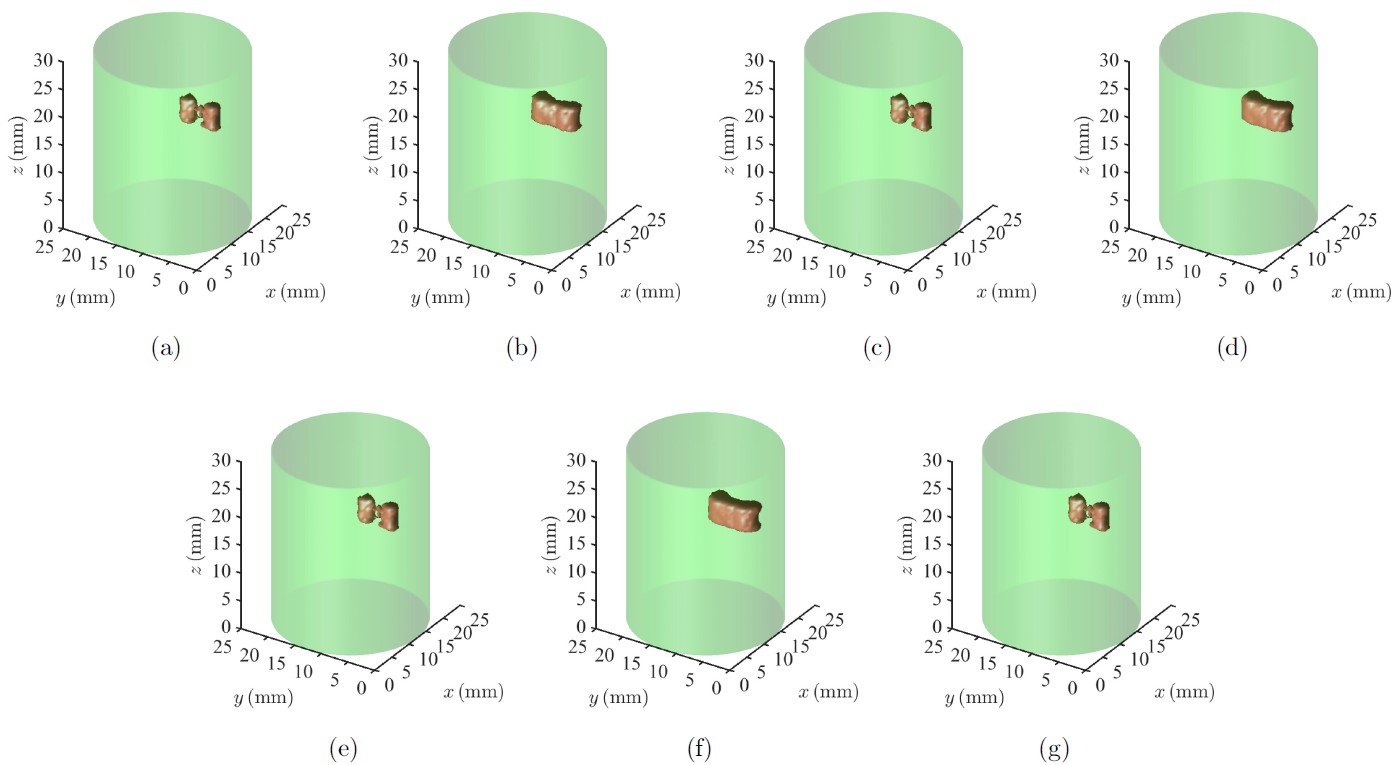
图12：3D仿真实验重建图像（荧光目标较浅，间距2.5mm，25%噪声）。（a）RIGA-R。（b）（c）ACPM。（d）（e）POGM。（f）（g）FISTA-R。（a）（c）（e）（g）采用相同的算法终止判据。（b）（d）（f）采用与RIGA-R相同的迭代次数。

图7-图12中的3D仿真实验重建图像表明，如果采用相同的算法终止判据，本文提出的RIGA-R算法相比于其它三种算法能获得几乎完全一样的重建图像，但是只需要明显更少的迭代次数。

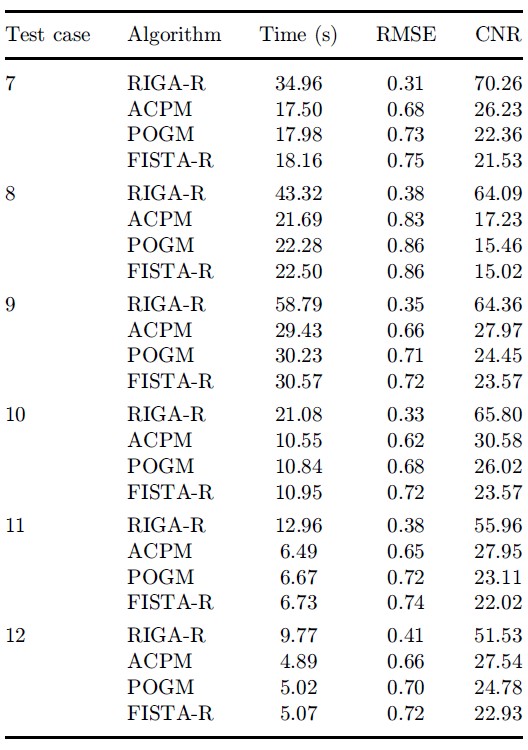
表3：3D仿真实验重建定量结果（四种算法采用相同的迭代次数）。

表3说明，3D仿真实验中，如果采用相同的迭代次数，本文提出的RIGA-R算法获得的图像重建精度（RMSE和CNR）远高于其它三种算法。

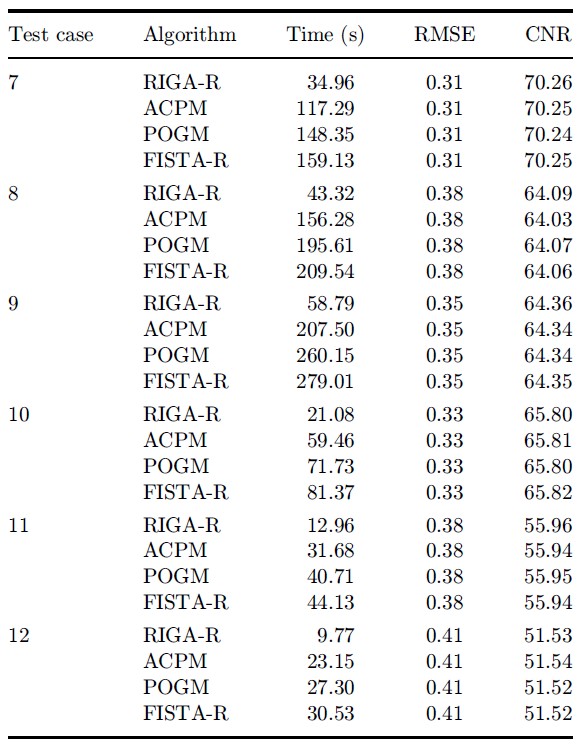
表5：3D仿真实验重建定量结果（四种算法采用相同的终止判据）。

表5说明，3D仿真实验中，如果采用相同的算法终止判据，本文提出的RIGA-R算法获得的图像重建精度（RMSE和CNR）与其它三种算法几乎完全相同，但是重建速度远快于其它三种算法。

通讯作者简介

王雷，哈尔滨工程大学物理与光电工程学院基础教学研究中心副教授。在长期讲授《大学物理》课程的同时，也从事生物医学光子学方向的一些研究。以第一或通讯作者发表SCI论文4篇。